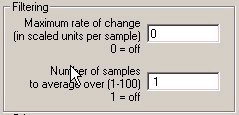
Variable Filtering
In the test and racing environment it is quite common that the sensor outputs will have some noise on them - the most common cause for this is noise picked up from the vehicle ignition system. Using good electrical installation practices the noise can be greatly reduced, but in practical situations it is often impossible to eliminate altogether.
As a "second line of defence" there are filtering features incorporated within the display products. You can use these options to "clean up" the data if you find that the displayed information is either jumping between values, or that the alarms are triggering unexpectedly.
There are 2 separate filter options provided that work in 2 different ways:
1. You can set a maximum rate of change for each variable. This is ideal for rejecting spikes from variables that change quite slowly - a simple example is air temperature. If we know that the temperature of the air can never change faster than 1 degree per second and we are sampling it at 10Hz then we should enter 0.1 in the box. If there is then a large spike on the data, say 20 - 20 - 78 - 20 - 20, then this would be almost completely eliminated, so it would result in 20 - 20 - 20.1 - 20 - 20.
2. The second type of filtering is a more conventional smoothing filter which outputs the average of a batch of samples, rather than an individual value. The more samples you average over the slower and smoother the response. The value should be set as appropriate for the sensor response time, again in the case of the air temperature sensor the response time is about 5 seconds and so if we were sampling at 10Hz it would be reasonable to filter over 50 samples.
In practice you should use both filters in combination to provide clean/smooth data to display but you should make sure that the data is as good as possible with good electrical installation practices first.
Also note that both the filters are dependent on the sample frequency of the data - if you change the sample frequency then this will have an effect on the filtering.
Also note that because of the way the averaging filter works, the number of samples averaged is approximate.