RPM And Wheel Speed
Inputting the correct number of pulse per engine revolution here allows the software to correctly scale your RPM input.
Ignition Pulses Per Revolution:
Setting the RPM pickup parameters enables the software to translate the number of ignition pulses into the correct engine speed. To do this, you will need to know how many pulses per engine revolution the RPM pickup will record. This will vary depending on where the RPM pickup is situated.
| Ignition system | Pulses per revolution |
| Coil per plug | 0.5 |
| Wasted spark | 1 |
| Distributor (sensor on plug lead) | 0.5 |
| Distributor (sensor on king lead) | Number of cylinders /2 |
User defined function for wheel speed:
There are 2 standard variables for speed in the analysis software, “Speed” and “Wheel Speed”. Speed is used thoughout the software and used to calculate distance, and track maps. Wheel speed is from the vehicles wheels and typically only used in specialist applications.
Because there are 4 frequency inputs on the DL1, there are many ways that the user may want to calculate wheel speed on the DL1. To allow maximum flexibility, the software allows you to enter a formula to define wheel speed. For example, if you have a single wheel speed sensor attached to a wheel with 5 pulses per revolution and a rolling radius of 2.1m and the input goes to the first frequency channel then:
Wheel Speed [kph] = VAR_38 / 5 *2.1 * 60 * 60 / 1000
VAR_38 is the input in Hertz /5 because there are 5 pulses per wheel revolution, *2.1 because you move 2.1m for each wheel rev, *60*60/1000 to convert from m/s to kph. If there is a wheel speed sensor attached to each wheel, then the formula could take an average value of the frequencies or a minimum or maximum value as desired. For more information on user defined channels, look here. Note that any frequency (or other) inputs that you use to calculate wheel speed from must be available in the variable manager, for example:
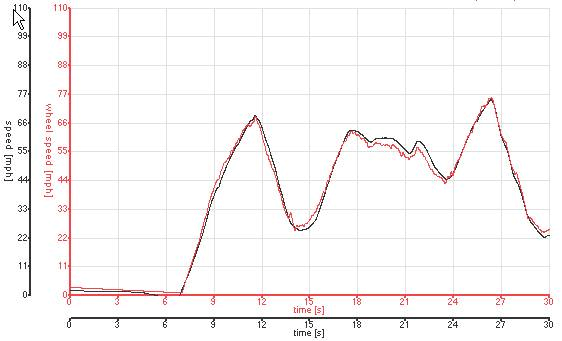
Once you entered an equation for wheel speed, it is best to check that the scaling has been calculated correctly. To do this the simplest thing to do is to plot a graph of wheel speed and “normal” speed and compare them to make sure they are very similar. For example:
If there are any significant scaling differences, then please check the equation that was used to convert to a wheel speed.